Semileptonic decays

One of the simplest and most common beauty quark decays is the charged-current transition into a charm quark, where the W boson decays into two leptons. For example, the decay of a B meson into a D meson, a charged lepton, l, and a neutrino, ν, as shown in Figure 1.

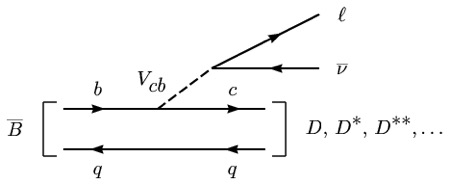
Figure 1. The decay of a B meson into a charmed meson (denoted D, D*, D** depending on the excitation). The decay is mediated by the W boson in the Standard Model which decays into a lepton, l, and a neutrino, ν.

The advantage of semileptonic decays is that the interaction of strong force in the decay can be reliably predicted. This means that the behaviour of such decays can be compared to what one would expect assuming only the W boson is responsible for the decay. If the behaviour is different then it indicates that there are new additional particles mediating the decay which would be a leap in understanding in particle physics.

One very distinctive feature of the W boson is that it couples equally to the different types of leptons, a concept known as lepton uniersality. Tests of lepton universality in semileptonic beauty quark decays are highly sensitive to new particles which, for example, couple preferentially to the heavier tau particle compared to the electron or muon. Measurements of the ratio of the decay rate of B→D^(*)τν with respect to B→D^(*)lν have shown a discprency with predictions, perhaps indicating that its not only the standard W boson involved in the decay (see Figure 2).

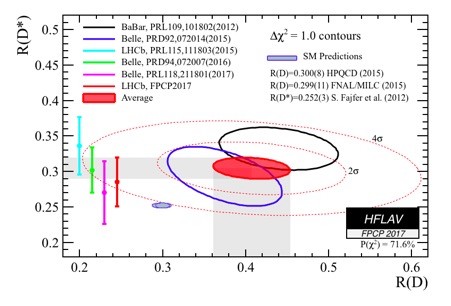
Figure 2. Summary of the measurements of the lepton universality ratios R(D) and R(D^*) as of July 2017. The combined experimental fit is approximately four standard deviations from the Standard Model.

Our group is currently involved in new tests of lepton universality, such as measurements in beauty baryons. These decays are important to cross-check experimental and theoretical uncertainties. If a deviation is seen in baryons as well, then it will provide confidence that there is an effect from new particles rather than the more mundane explanation of a statistical fluke or underestimated uncertainties.

A few selected publications are listed below:

Test of lepton universality with B⁰→K^*0l⁺l^- decays

Lepton flavour universality tests using semitauonic decays at LHCb

Measurement of an excess of B→D^(*)τν decays and implications for charged Higgs bosons

Measurement of the tau lepton polarization and R(D^*) in the decay  B → D^*τ^- ν _τ

Measurement of the ratio of branching fractions B( B ⁰→D^*+τ^- ν _τ) / B( B ⁰→ D^*+μ^- ν _μ)