Navigation auf uzh.ch
Navigation auf uzh.ch
In their latest PRL work, the Bzdušek group formulates a novel method for efficient modelling of hyperbolic lattices. Simultaneously, two associated software packages have been publicly released to make the technique accessible to the broader community.

Hyperbolic lattices
While solid-state physics has traditionally focused on crystalline materials, i.e., periodic structures in flat space, recent experiments with metamaterials (cf. also our previous experimental work) have enabled emulations of the negatively curved hyperbolic space. The resulting "hyperbolic lattices" constitute at present a largely unexplored territory, and their spectral and quantum mechanical properties imply unique challenges on account of the curvature-induced noncommutativity of hyperbolic translations. Hyperbolic lattices were recently theoretically described by a non-Abelian generalization of the Bloch theorem, but practical approaches for efficient computations have remained missing.
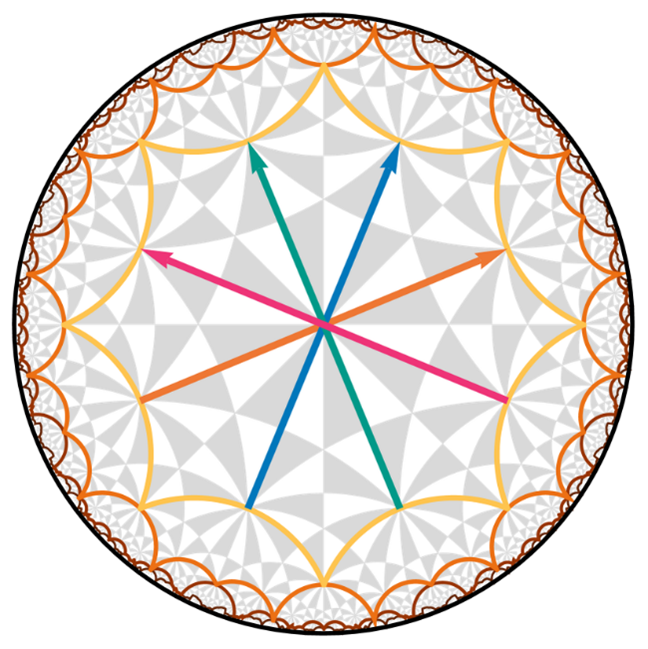
Figure 1:The primitive unit cell (yellow) with translation generators (colored arrows) and a coherent sequence of supercells (shades of brown) for the hyperbolic {8,3} lattice.
Efficient description through supercells
Our proposed “supercell method” [1] overcomes the challenges posed by noncommuting translations, and enables significant progress towards an analytical description of hyperbolic lattice models in momentum space. Specifically, we use computational group theory to create a sequence of progressively larger unit cells, each formed as a symmetric aggregate of smaller unit cells. We apply the previously established Abelian hyperbolic band theory — which ignores the noncommutativity of translations — to those growing supercells and obtain a converging description of the infinite lattice. The illustration below showcases the modelling and the extracted converging spectra for the hyperbolic Haldane model.
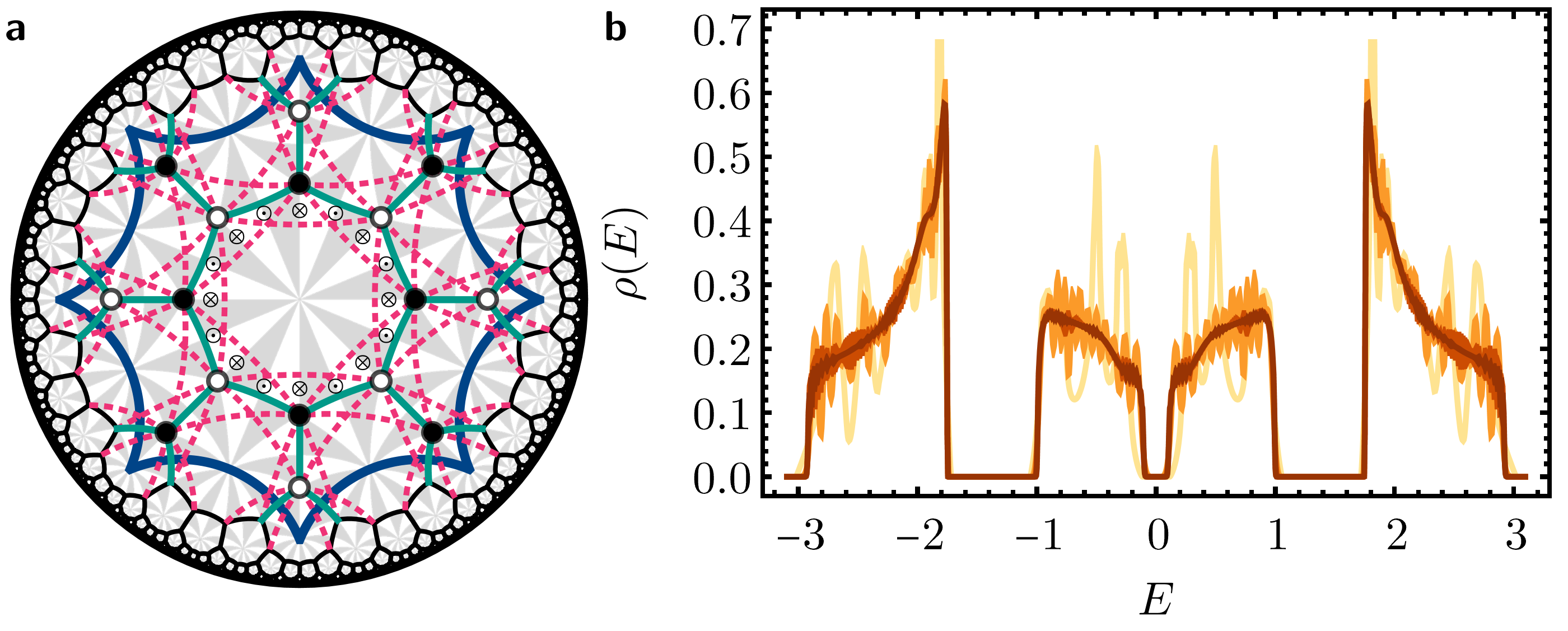
Figure 2: Haldane model on the hyperbolic {8,3} lattice (left) and the converging data for density of states (right) with broad topological gaps.
This advancement not only deepens our theoretical understanding but also enhances our capability to simulate hyperbolic lattices computationally. Our results represent a pivotal step towards a comprehensive band-theoretic characterization of hyperbolic lattices and open the door to exploring previously inaccessible aspects of their properties.
Software packages
To encourage further investigations in this emerging field, we have implemented the supercell method in a pair of complementary open-source software packages.
The first package, called HyperCells [2], is implemented in GAP — a programming language with particular emphasis on computational group theory. The package allows to construct symmetric unit cells and supercells of regular hyperbolic lattices. This aids in defining models on such lattices and utilizing their symmetries. Additionally, the package outputs appropriate periodic boundary conditions (which is a nontrivial task in hyperbolic lattices) for various system sizes and the necessary information for applying our supercell method.
The second package, called HyperBloch, is implemented in Mathematica. It can read the output of the HyperCells package, visualize it, and provides an interface for defining concrete tight-binding models. In particular, it allows an easy application of the supercell method to those models to construct hyperbolic Bloch Hamiltonians and to compute their energy spectra.
References
[1] P. M. Lenggenhager, J. Maciejko, and T. Bzdušek, Non-Abelian hyperbolic band theory from supercells, Phys. Rev. Lett. 131, 226401 (2023).
[2] P. M. Lenggenhager, J. Maciejko, and T. Bzdušek, HyperCells: A GAP package for constructing primitive cells and supercells of hyperbolic lattices, 10.5281/zenodo.10222598 (2023).
[3] P. M. Lenggenhager, J. Maciejko, and T. Bzdušek, HyperBloch: A Mathematica package for hyperbolic tight-binding models and the supercell method, 10.5281/zenodo.10222865 (2023).
Katharina Mueller