Anderson localization
Phase transition of waves in random media
When waves diffuse through a random medium, the mean free path is no longer the only length scale determining the physical situation. Due to interferences, additional effects will appear on the scale of the wavelength, lambda. A striking prediction made by Anderson in 1958 is that in fact diffusion should come to a halt in a medium where the mean free path is comparable with the wavelength. In the context of electronic systems, this has been used as an explanation for the transition from metallic to insulating behaviour with the addition of impurities. We study this phenomenon for the case of diffusing photons in a system made of particles with a high refractive index on the scale smaller than the wavelength of light. Here, localization can be observed without the complications induced by electron-electron, as well as electron-atom interactions, thus allowing a study of pure Anderson localization.
Deviations from classical diffusion
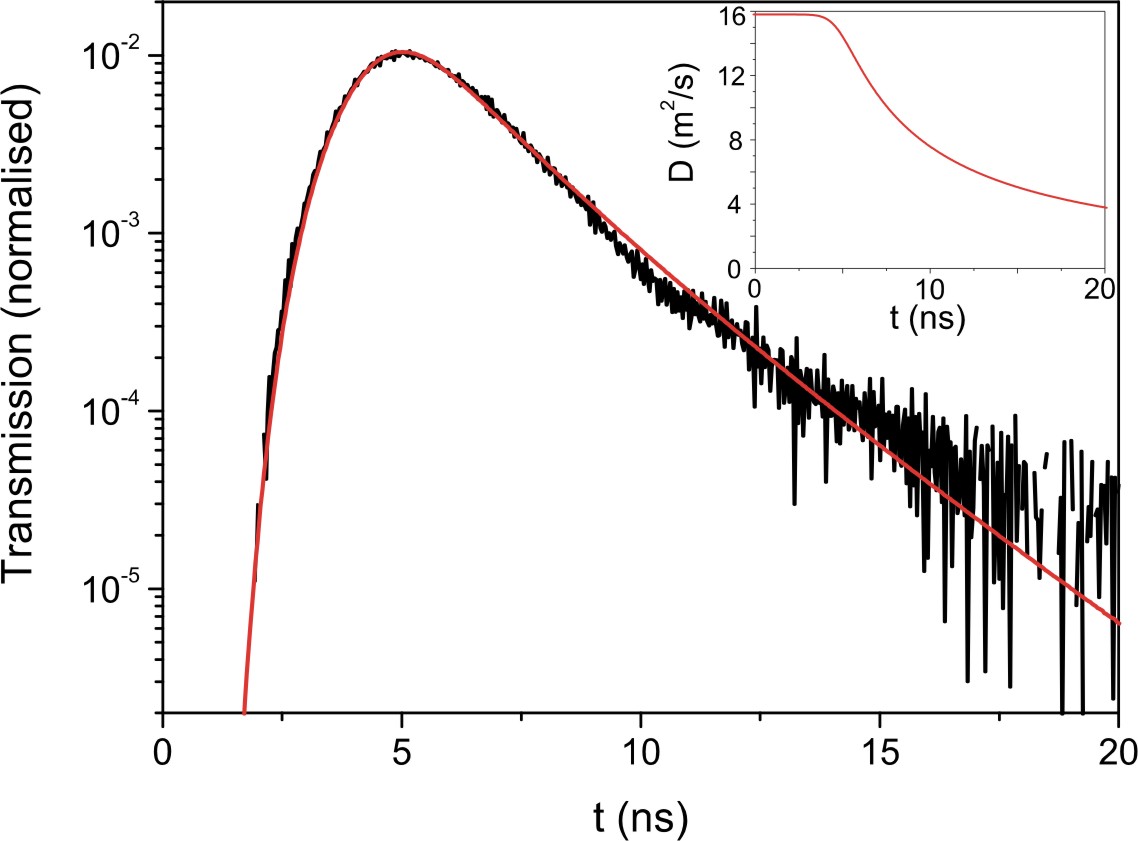
Time-resolved measurements in contrast can specifically look for long paths, where localization should occur and thus test for the hypothesis of a scale dependent diffusion coefficient. We carry out measurements of time-resolved transmission of a picosecond pulse through a multiple-scattering sample. For samples with very high turbidity (characterized by a low value of the mean free path l* - and measured from the width of the coherent backscattering cone), we observe increasing deviations from the behaviour of classical diffusion of a light-pulse [Stoerzer et al. Phys. Rev. Lett. 96, 063904 (2006)].
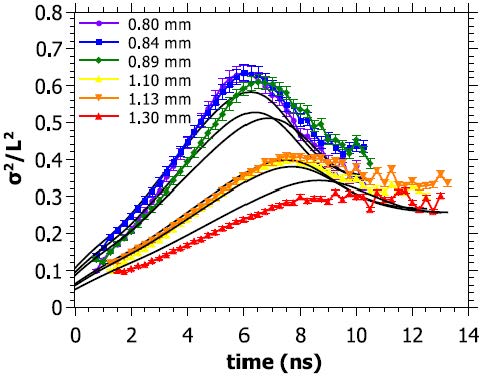
Using sub-nanosecond scale imaging, it is possible to determine the spatial distribution of photons leaving the turbid sample as a function of time. Here again, we have found deviations from diffusion with a saturation of the width of the photon distribution in time. This would not be present in diffusive processes, which lead to an absorption independent linear increase in the width of the exiting photons. A direct image of this is shown in the image below, where the increase of the width at late times can be seen to come to a halt.
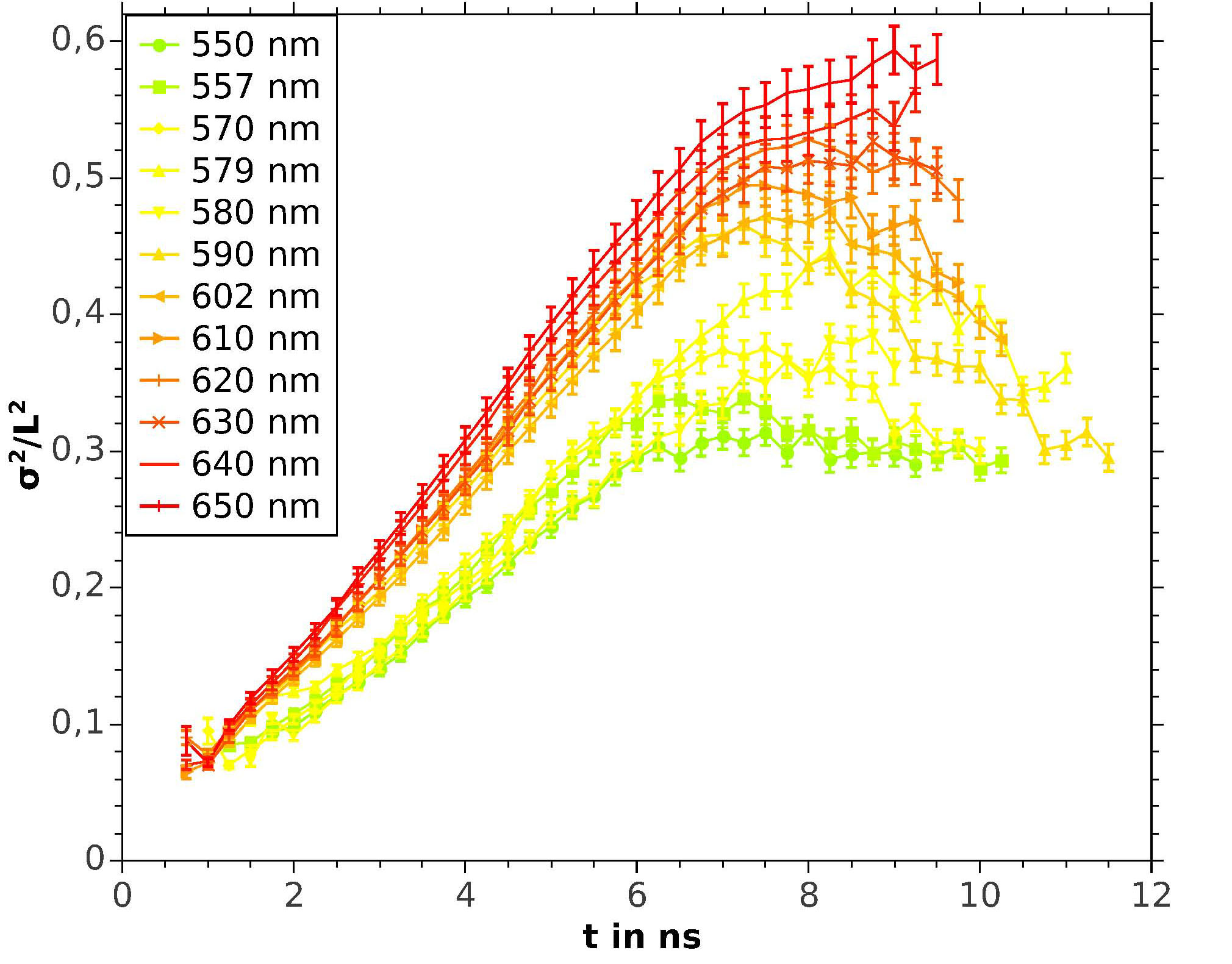
The temporal development of the width shows a plateau in localizing samples after an initial linear increase corresponding to diffusion of light at early stages. The transition in three dimensions with turbidity can then be scanned by a change in the wavelength used, which is shown in the figure below for one and the same sample. At the lowest values of kl* = 2, corresponding to the lowest wavelengths, the width saturates, whereas at higher values of kl* = 4.5, corresponding to the highest wavelength, the width increases at all times measures, albeit with a change to non-linear behaviour at late times.
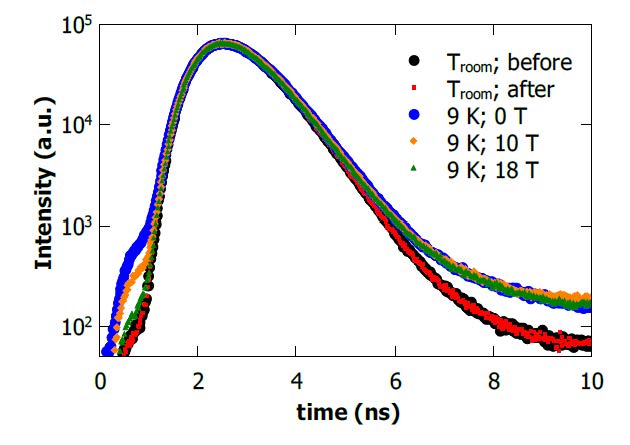
Testing the influence of path reciprocity using Faraday rotation in the sample
As path reciprocity lies at the base of Anderson localization a direct test of localization lies in the destruction of path reciprocity, which is possible using Faraday active materials in the scatterers and the application of a strong magnetic field. The results of a time of flight experiment in such a case are shown in the figure below, where no influence of the magnetic field has been observed in spite of the fact that the combined Verdet constant and applied magnetic field should be strong enough for an effect to be present.
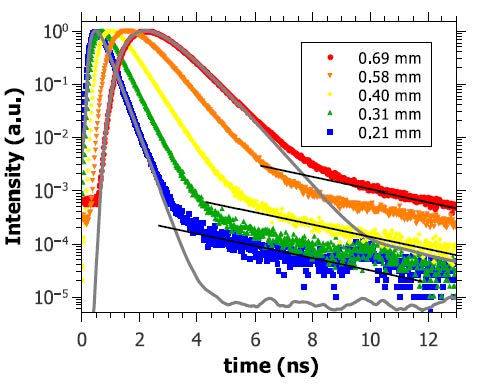
Thickness dependence of deviations from diffusion
If the deviations from diffusive light transport are due to localization, then the saturation width would correspond to the localization length, such that samples thinner than this length should not show localization effects any longer. Producing such thinner samples in a still homogeneous fashion can then shown whether the deviations are due to localization or not. This is shown in the figure below, where it can be seen that deviations at long times are also present in very thin samples.
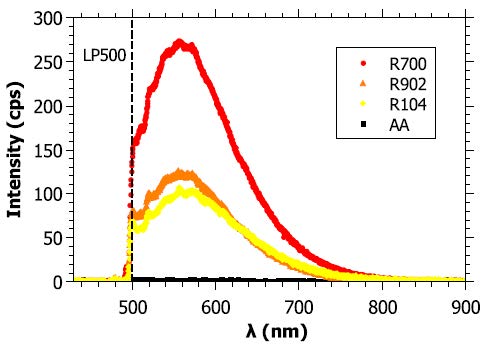
Inelastic processes in the samples showing deviations from diffusion
Using wave-length dependent measurements, one finds that there are inelastic processes at play in the samples, such that wave-length shifted photons leave the samples at long times.
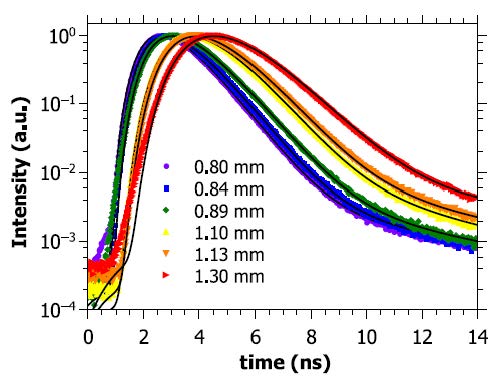
Delayed fluorescence model to explain the deviations from diffusion
Introducing a time-delayed process corresponding to the life time of the inelastic processes observed into a classical diffusion model, one can predict the time-of flight measurements as well as the time-dependent saturation of the width of the photon cloud quantitatively. This is shown below and demonstrates that small fluorescent contributions in the samples can explain all of the deviations from diffusive behaviour we have observed.